Produit scalaire dans l'espace

L'incontournable du chapitre est la notion de produit scalaire. Tu l'as abordée en 1^re dans le plan, et ici tu l'abordes dans l'espace. Elle est essentielle car elle parle de l'orthogonalité en particulier.

Rappel sur les vecteurs colinéaires

• 2 vecteurs ^→u et ^→v sont colinéaires, si et seulement si il existe un réel λ tel que ^→u = λ^→v. Exemple :

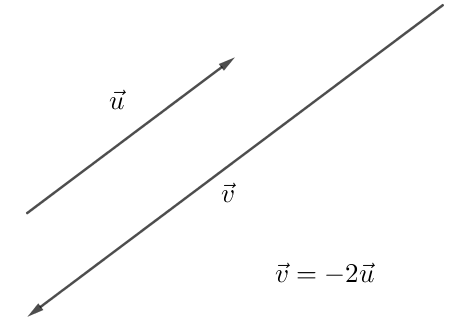
• Propriétés

2 vecteurs ^→u et ^→v colinéaires et non nuls ont la même direction.

3 points A, B et C sont alignés si et seulement si les vecteurs ^→AB et  ^→AC sont colinéaires.

Le vecteur nul est colinéaire à tout autre vecteur.

Exemple :

Les vecteurs ^→u (2;3;1) et ^→v (−6;9;−3) sont colinéaires car ^→v = −3 x ^→u.

Les vecteurs ^→u (2;−3;1) et ^→v (4;−6;−2) ne sont pas colinéaires car : 

2 x 2 = 4 ;  2 x (−3) = −6  mais   2 x 1 ≠ −2.

Quelle est la définition du produit scalaire ?

La définition du produit scalaire est la suivante : dans l’espace, une unité de longueur étant choisie, on a pour tous vecteurs^→u et ^→v  :

Coordonnées

On considère les deux vecteurs ^→u (x;y;z) et ^→v (x′;y′;z′), le produit scalaire de ^→u et de ^→v est le réel :

^→u .^→v  = xx′ + yy′ + zz′.

Théorème

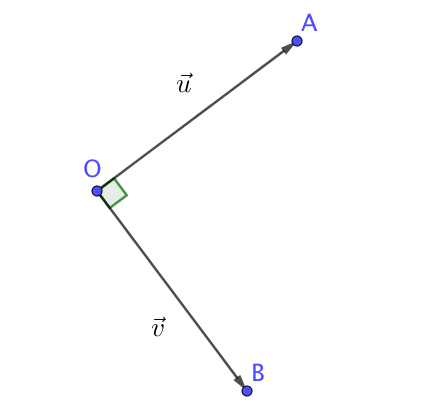
Soient deux vecteurs ^→u et ^→v non nuls et trois points O, A et B tels que ^→u = ^→OA et ^→v = ^→OB.

Les 3 propositions suivantes sont équivalentes :

(OA) et (OB) sont perpendiculaires,

^→u ⋅ ^→v = 0

^→u et ^→v sont orthogonaux : on notera ^→u ⊥ ^→v.

Exemple :

On considère les vecteurs ^→u (1;3;1) et ^→v (4;1;−7). Sont-ils orthogonaux ?

On calcule leur produit scalaire :

^→u ⋅ ^→v = 1 x 4 + 3 x 1 + 1 x (−7) = 0

^→u et ^→v  sont donc orthogonaux car leur produit scalaire est nul.