
Aimé à 100% par nos utilisateurs

Regarde cette vidéo et gagne facilement jusqu'à
 15 Lumniz
en te connectant !
15 Lumniz
en te connectant !
Il n’y a pas de Lumniz à gagner car tu as déjà vu ce contenu. Ne t’inquiète pas, il y a plein d’autres vidéos, jeux, quiz ou articles intéressants à explorer et toujours plus de Lumniz à remporter.
Gravitation universelle
Les bons profs : physique-chimie Collège
I. Loi de la gravitation
Cette loi dit que deux corps qui ont une masse s’attire mutuellement.
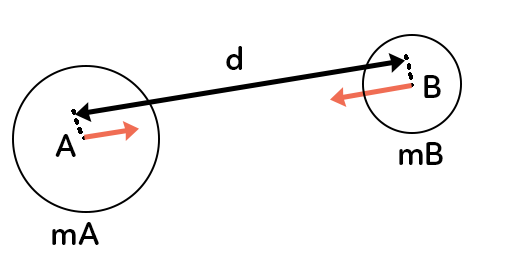
Par exemple, on a représenté un corps A avec une masse mAmA et un corps B qui a une masse mBmB.
- A attire B et B attire A.
Cette attraction est représentée par la force qui est la flèche représentée sur le schéma. La flèche en A représente l’attraction de B sur A. B attire A vers lui. Et la flèche en B représente l’attraction exercée par A sur B. A attire B vers lui.
- Pour calculer l’intensité ou valeur de cette force, il y a une formule que l’on ne doit pas savoir par cœur mais que l’on doit savoir appliquer. On va donner la formule dans les exercices et on devra savoir remplacer les termes dans la formule par leur valeur. Cette formule est la suivante :
F = (G x mA x mB)/d2
Dans cette formule G est une constante qui sera donnée et qui vaut G = 6,67 x 10-11 Nm2/kg2 ; mA est la masse du premier corps exprimée en kg ; mB est la masse du deuxième corps exprimée en kg et d est la distance au carré qui doit être exprimée en m.
II. Exemple
Calculer l’intensité ou la valeur de la force gravitationnelle exercée par la Terre sur la Lune, puis par la Lune sur la Terre.
On a les masses suivantes : mTerre = 5,98 x 1024 kg, mLune = 7,35 x 1022 kg. Et la distance Terre-lune est de dTL = 3,84 x 105 km.
Pour calculer la valeur ou intensité de cette force, il suffit de remplacer mA et mB par la mTerre et mLune, et d par dTL au carré.
Dans le calcul, cela fait : F = (6,67 x 10-11× 5,98 x 1024 x 7,35 x 1022)/dTL2.
Attention, il existe un piège car dTL est en kilomètres et la distance doit être en mètres. Pour la convertir en mètres, il faut multiplier par 1000.1000. On peut aussi utiliser un tableau de conversion si on a des difficultés avec la conversion.
Donc, on a : F = (6,67 x 10-11× 5,98 x 1024 x 7,35 x 1022)/((3,84 x 105 x 1000)2)
Sur la calculatrice, il faut bien mettre des parenthèses au numérateur et au dénominateur pour ne pas avoir de problème au niveau du résultat. Si on fait le calcul ici, on trouvera 2 x 1020 N (car l’unité des forces est le Newton).
Si maintenant on veut l’intensité de la force exercée par la lune sur la Terre, c’est très simple, ces deux forces ont la même intensité. Donc, elle sera tout simplement égale à 2 x 1020 N.
Réalisateur : Les Bons Profs
Producteur : Les Bons Profs
Année de copyright : 2016
Année de production : 2016
Publié le 18/06/19
Modifié le 06/01/25
Ce contenu est proposé par




